Lecția 6. M U L Ț I M EA NUMERELOR RAȚIONALE (II) – pregătirea Evaluării Naționale 2020
Fracții echivalente
Două fracții mn și pq se numesc echivalente dacă sunt egale, adică au aceeași reprezentare. (valorile rapoartelor sunt egale)
Exemple: 12=36 (valoarea comună este 0,5); -59=-1018 (valoarea comună este -0,(5)); mn=pq⇔m·q=n·p
Fracțiile echivalente cu o fracție dată se obțin prin simplificare sau amplificare.
Număr rațional
Numerele raționale sunt fracțiile ireductibile, adică putem defini mulțimea numerelor raționale ca fiind ℚ=mn|m,n∈ℤ,n≠0,m.n=1
Exemplu: 25 este fracție ireductibilă pentru că (2, 5,)=1, deci reprezintă numărul rațional = 0,4615 este tot numărul rațional 25 pentru că (6, 15)=3, deci 615(3=25=0,4
Transformarea fracțiilor
Pentru a transforma o fracție ordinară în fracție zecimală, efectuăm împărțirea (numărătorul îl împărțim la numitor)
Exemplu: -12=-0,5
Pentru a transforma o fracție zecimală finită în fracție ordinară folosim formula a0,a1a2…an⇀=a0a1a2…an1000…0,a0∈ℤ, a1, a2,…an cifre (sunt n cifre de 0 la numitor)
Exemplu: 12,34=1234100(2=61750
Pentru a transforma o fracție zecimală periodică simplă în fracție ordinară folosim formula a0,a1a2…an=a0a1…an-a099…9,a0∈ℤ,a1, a2,…an cifre (sunt n cifre de 9 la numitor)
Exemplu: 12,34=1234-1299=122299
Pentru a transforma o fracție zecimală periodică mixtă în fracție ordinară folosim formula a0,a1a2anb1b2…bm=a0a1…anb1b2…bm=a0a1…an99…900…0, a0∈ℤ,a1,a2,…an,b1,b2,…,bm cifre (sunt m cifre de 9 și n cifre de 0 la numitor)
Exemplu: 1,2(34)=1234-12990=1222990(2=611495
Compararea numerelor raționale
pentru a compara două fracții ordinare, avem nevoie să aibă același numitor (de obicei). ab≤cb⇔a≤c(b > 0)
Exemple: 35≤75 pentru că 3≤7; -23=-23≤-13=-13;
OBS: Dacă nu avem același numitor, aducem fracțiile la același numitor.
pentru a compara două fracții zecimale, comparăm părțile întregi. Dacă sunt diferite, putem stabili deja că numărul cu partea întreagă mai mare este mai mare.
Dacă sunt egale părțile întregi, comparăm, pe rând, fiecare zecimală până găsim o pereche diferită (dacă nu sunt zecimale diferite, atunci numerele vor fi egale), zecimala mai mare ne va indica numărul mai mare (pentru numere pozitive), zecimala mai mică ne va indica numărul mai mare (pentru numere negative).
Exemple:
12,34 > 10,345 (pentru că 12 >10)
-3,24 < -1,9 (pentru că -3 < -1)
0,12 < 0,2 (pentru că 0 = 0, 1 < 2 , numere pozitive)
– 5,12 > – 5,2 (pentru că -5 = -5, 1 < 2 , numere negative)
1,2(3) = 1, 23333…> 1,2323…= 1,(23)
– 5,42(7)= -5,42777… < -5, 427 ( 42777…> 427, numere negative )
Riscuri (greșeli)
– să confundăm formulele de la transformările fracțiilor zecimale în fracții ordinare
KIDI- sfat: să efectuăm verificarea ( împărțirea – adică transformarea inversă)
să confundăm fracția cu numărul rațional
KIDI- sfat: întotdeauna rezultatele trebuie să fie scrise sub formă de fracție ireductibilă; acela este numărul rațional.
Felicitări! Ai terminat cursul!
„A N T R E N A M E N T U L KIDI-10”
Rezumat chestionar
0 din 10 întrebări finalizate
Întrebări:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Informații
.
 Ufo eat all the school library. Can you prove her that you are smarter?
Ufo eat all the school library. Can you prove her that you are smarter? Dacă vrei să-ți salvezi punctele câștigate și să apari în topurile Kidibot, trebuie să fii logat(ă). Creează-ți aici un cont sau loghează-te.
Great! To see your results, you must create your Kidibot FREE account (or login here ). This way, you’ll not loose the points you won for this quiz.
Ai finalizat deja chestionarul mai înainte. De aceea nu-l poți relua.
Chestionarul se încărcă...
Trebuie să te autentifici sau să te înregistrezi pentru a începe chestionarul.
Trebuie să termini următorul chestionar pentru a începe acest chestionar:
Rezultate
0 din 10 întrebări au răspunsuri corecte
Durată de răspuns:
Timpul a trecut
Ai obținut 0 din 0 de puncte posibile, (0)
| Scor mediu |
|
| Scorul tău |
|
Categorii
- Fără categorie 0%
-
-
Din păcate, nu ai răspuns corect de suficient de multe ori. Așa că nu ai primit nici un punct. Fii mai atent data viitoare.
| Poz. | Nume | Introdus pe | Puncte | Rezultat |
|---|---|---|---|---|
| Tabelul se încărcă | ||||
| Nicio dată disponibilă | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Cu răspuns
- Reia
-
Întrebarea 1 din 10
1. Întrebare
1 puncteDintre fracțiile , echivalente suntCorect
Incorect
-
Întrebarea 2 din 10
2. Întrebare
1 puncteA,(a)=Corect
Incorect
-
Întrebarea 3 din 10
3. Întrebare
1 puncte1,ab < 1,(b) AtunciCorect
Incorect
-
Întrebarea 4 din 10
4. Întrebare
1 puncte, a. AtunciCorect
Incorect
-
Întrebarea 5 din 10
5. Întrebare
1 puncteNumerele reprezintăCorect
Incorect
-
Întrebarea 6 din 10
6. Întrebare
1 puncteAtunciCorect
Incorect
-
Întrebarea 7 din 10
7. Întrebare
1 puncte. AtunciCorect
Incorect
-
Întrebarea 8 din 10
8. Întrebare
1 puncteCel mai mare dintre numerele a,12; a,1(2); a,(2), a,(12) ( cu a< 0 ) esteCorect
Incorect
-
Întrebarea 9 din 10
9. Întrebare
1 punctePentru fracția existăCorect
Incorect
-
Întrebarea 10 din 10
10. Întrebare
1 punctePentru fracția existăCorect
Incorect
Exemple de întrebări din quizul "Lecția 6. M U L Ț I M EA NUMERELOR RAȚIONALE (II) – pregătirea Evaluării Naționale 2020"
- . Atunci
- 1,ab < 1,(b) Atunci
- Numerele reprezintă





 GAME OF TRONES- THE MOVIE
GAME OF TRONES- THE MOVIE Curiozități despre Terra
Curiozități despre Terra INMULTIREA CU 700 !!!
INMULTIREA CU 700 !!! Am pus la încercare cerul
Am pus la încercare cerul Harry Potter Trivia
Harry Potter Trivia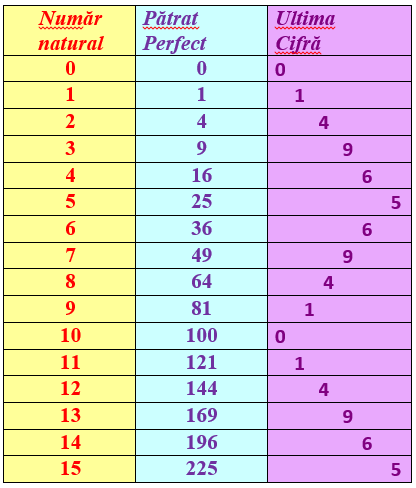 Patratul perfect al unui numar natural
Patratul perfect al unui numar natural Piticii şi matematica (5) .
Piticii şi matematica (5) . Cine a fost Albert Einstein?
Cine a fost Albert Einstein?









